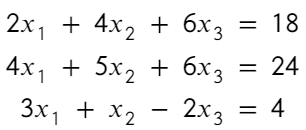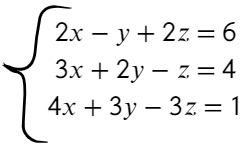Formalmente, si A es una matriz cuadrada no-singular, es decir, tal que su determinante es distinto de cero. Podemos usar el Método de Eliminación de Gauss-Jordan para calcular la solución del sistema de ecuaciones ampliando la matriz A adosando la matriz de términos independientes C a su lado derecho.

La técnica más común para resolver el sistema de ecuaciones lineales es la de hacer uso de un procedimiento para la eliminación sucesiva de las incógnitas denominado método de Gauss. Describiremos la aplicación de este método para un sistema de cuatro ecuaciones con cuatro incógnitas y posteriormente, la generalizaremos para un sistema de n...

La restricción de que el determinante de la matriz debe ser diferente de cero para la existencia de la matriz inversa es debido a la imposibilidad de dividir por cero. Dicha condición, a diferencia de la de inversibilidad, sí que es necesaria y suficiente; esto es, podemos afirmar que toda matriz cuyo determinante sea diferente de cero tiene...

El cálculo de la matriz inversa por el método de Gauss supone transformar una matriz en otra, equivalente por filas. La demostración rigurosa del procedimiento que a continuación se describe se sale del propósito del presente bloque, aquí se limita a su exposición y comprobación de que efectivamente se obtiene la matriz inversa.